이 기사는 우리에게 FFT MATLAB에서.
FFT 이해
그만큼 고속 푸리에 변환(FFT) 신호를 다르게 이해하는 데 도움이 되는 특별한 기술을 나타냅니다. 일반적으로 신호는 시간이 지남에 따라 변하는 일련의 숫자로 표시되지만 FFT, 신호에 어떤 다른 주파수가 있고 얼마나 강한지 확인할 수 있습니다. 신호를 음표로 분해하고 각 음표의 크기를 확인하는 것과 같습니다.
그만큼 FFT 알고리즘은 신호 데이터에 대해 많은 복잡한 수학을 수행합니다. 신호를 받아 더 작은 부분으로 나눈 다음 각 부분의 주파수와 강도를 계산합니다. 마지막으로 모든 결과를 결합하여 신호의 주파수 내용, 위상 관계 및 기타 중요한 특성에 대한 그림을 제공합니다.
이 기술은 신호를 더 잘 분석하고 이해하는 데 도움이 되기 때문에 많은 분야에서 사용됩니다. 예를 들어, 신호 처리 , 우리는 사용할 수 있습니다 FFT 원치 않는 노이즈를 걸러내거나 특정 패턴을 감지합니다. ~ 안에 오디오 분석 , 다양한 소리를 식별하거나 오디오 녹음 품질을 분석할 수 있습니다. ~ 안에 이미지 처리 , FFT 이미지의 공간 주파수를 분석하는 데 도움이 될 수 있습니다. 그리고 통신 분야에서는 FFT 신호를 효과적으로 송수신하는 데 사용됩니다.
MATLAB에서 FFT를 사용하는 방법
MATLAB은 다음과 같은 내장 함수를 제공합니다. fft 우리가 수행할 수 있게 해주는 고속 푸리에 변환(FFT) 신호에 대한 계산. 이 기능은 사용하기 쉽고 주파수 영역에서 신호를 분석하고 조작하기 위한 다양한 옵션을 제공합니다.
사용을 위한 구문 FFT MATLAB의 함수는 다음과 같습니다.
에프 = fft ( 엑스 )에프 = fft ( x,n )
에프 = fft ( x,n,딤 )
여기:
에프=에프티(엑스) 의 계산을 산출합니다. 이산 푸리에 변환(DFT) 를 사용하여 x의 고속 푸리에 변환(FFT) 연산.
- x가 벡터를 나타내는 경우, fft(엑스) 벡터의 푸리에 변환을 산출합니다.
- x가 행렬을 나타내는 경우, fft(엑스) 각 열을 벡터로 취급하여 각 열의 푸리에 변환을 제공합니다.
에프 = fft(엑스,엔) n 포인트 DFT를 생성합니다. F는 값이 제공되지 않을 때 x와 동일한 크기를 가집니다.
- x가 벡터이고 길이가 n보다 작으면 x는 n에 도달할 때까지 후행 0으로 채워집니다.
- x가 벡터이고 길이가 n을 초과하면 해당 길이 n으로 잘립니다.
- x가 행렬인 경우 각 열은 벡터 케이스로 간주됩니다.
F = fft(x,n,딤) 주어진 차원 dim을 따라 푸리에 변환을 생성합니다. 의 말을하자, fft(x, n, 2) x가 행렬을 나타내는 경우 모든 행에 대해 n-포인트 푸리에 변환을 제공합니다.
다음 예제는 FFT MATLAB의 기능.
예 1
우리는 사용할 수 있습니다 FFT MATLAB에서 특정 주파수 구성 요소와 임의 노이즈가 있는 신호의 생성 및 분석을 시연합니다.
예를 들어:
ls = 2000년 ;fs = 1500 ;
TS = 1 /fs;
티비 = ( 0 :ls- 1 ) *ts;
에프 = 0.6 * 없이 ( 2 * 파이 * 오십 *TV ) + 삼 * 랜던 ( 크기 ( TV ) ) + 없이 ( 2 * 파이 * 120 *TV ) ;
구성 ( 1000 *TV ( 1 : 오십 ) ,에프 ( 1 : 오십 ) )
xlabel ( 'tv(밀리초)' )
라벨 ( '에프(tv)' )
제목 ( ' 평균 랜덤 노이즈가 0인 손상된 신호' )
에프 = fft ( 에프 ) ;
PS2 = 복근 ( 에프/ ls ) ;
PS1 = PS2 ( 1 : ls / 2 + 1 ) ;
PS1 ( 2 :끝- 1 ) = 2 *PS1 ( 2 :끝- 1 ) ;
에프 = 에프* ( 0 : ( ls / 2 ) ) / ls ;
구성 ( 에프, PS1 )
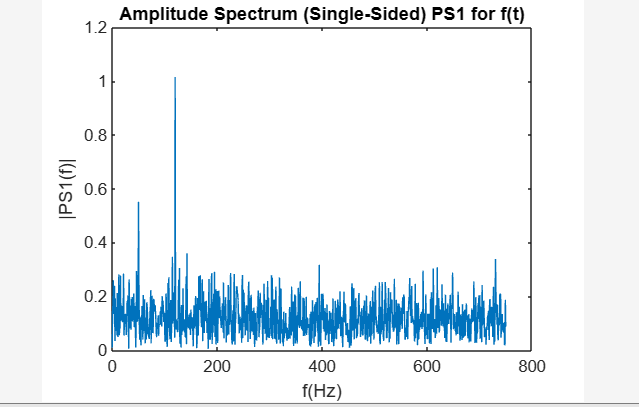
제목 ( 'f(t)에 대한 진폭 스펙트럼(단면) PS1' )
xlabel ( 'f(Hz)' )
라벨 ( '|PS1(에프)|' )
제공된 코드는 다음 길이의 신호를 생성합니다. 2000개 샘플(ls) , 샘플링 주파수 1500Hz(fs) , 그리고 샘플링 기간(ts) . 그만큼 시간 벡터(tv) 이 매개 변수를 기반으로 생성됩니다. 신호 에프 50Hz 및 120Hz의 정현파 구성 요소와 제로 평균 랜덤 노이즈의 조합으로 구성됩니다. 그런 다음 처음 50개 샘플의 세그먼트로 플롯됩니다. 코드는 다음을 추가로 계산합니다. FFT 신호의 진폭 스펙트럼(PS1) . 마지막으로 진폭 스펙트럼은 Hz 단위의 해당 주파수(f)에 대해 플롯됩니다.
예 2
다음은 FFT 시간 도메인을 통해 주파수 도메인으로의 가우시안 펄스 변환을 위한 MATLAB의 기능.
fs = 500 ;TS = - 0.5 : 1 /fs: 0.5 ;
ls = 길이 ( TS ) ;
에프 = 1 / ( 4 * 평방미터 ( 2 * 파이 * 0.02 ) ) * ( 경험치 ( -ts.^ 2 / ( 2 * 0.02 ) ) ) ;
구성 ( ts,f )
xlabel ( '시간(t)' )
라벨 ( '에프(티)' )
제목 ( '시간 영역' )
예 = 2 ^nextpow2 ( ls ) ;
에프 = 에프* ( 0 : ( 예/ 2 ) ) /예;
에프 = fft ( f,np ) ;
PF = 복근 ( F/NP ) ;
구성 ( f,PF ( 1 :예/ 2 + 1 ) )
xlabel ( '(에프)' )
라벨 ( '|PF(에프)|' )
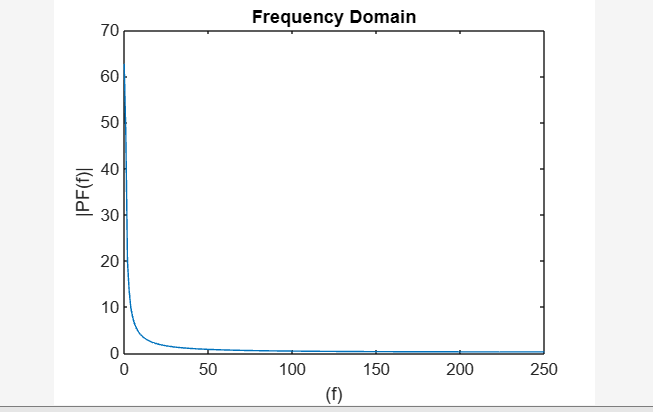
제목 ( '주파수 도메인' )
제공된 코드는 시간 영역에서 가우시안 펄스 신호를 생성하고 고속 푸리에 변환(FFT) MATLAB에서. 시간 도메인 신호가 플로팅된 다음 FFT 주파수 도메인 표현을 얻기 위해 수행됩니다. 결과 진폭 스펙트럼 해당 주파수에 대해 플롯됩니다.
예 3
다음 예제에서는 주파수가 서로 다른 3개의 정현파 신호를 생성하고 다음을 사용하여 시간 영역에 플로팅합니다. FFT MATLAB의 기능.
fs = 2500 ;TS = 1 /fs;
ls = 3000 ;
티 = ( 0 :ls- 1 ) *ts;
r1 = 없이 ( 삼 * 파이 * 60 *티 ) ;
r2 = 없이 ( 삼 * 파이 * 140 *티 ) ;
r3 = 없이 ( 삼 * 파이 * 350 *티 ) ;
에프 = [ r1; r2; r3 ] ;
~을 위한 케이 = 1 : 삼
서브플롯 ( 삼 , 1 ,케이 )
구성 ( 티 ( 1 : 250 ) ,에프 ( 케이, 1 : 250 ) )
제목 ( [ '행 번호' , num2str ( 케이 ) , '(시간 영역)' ] )
끝
예 = 2 ^nextpow2 ( ls ) ;
디 = 2 ;
에프 = fft ( f,np,d ) ;
PS2 = 복근 ( 에프/ ls ) ;
PS1 = PS2 ( :, 1 :예/ 2 + 1 ) ;
PS1 ( :, 2 :끝- 1 ) = 2 *PS1 ( :, 2 :끝- 1 ) ;
~을 위한 케이= 1 : 삼
서브플롯 ( 삼 , 1 ,케이 )
구성 ( 0 : ( fs/np ) : ( fs/ 2 -fs/np ) ,PS1 ( 케이, 1 :예/ 2 ) )
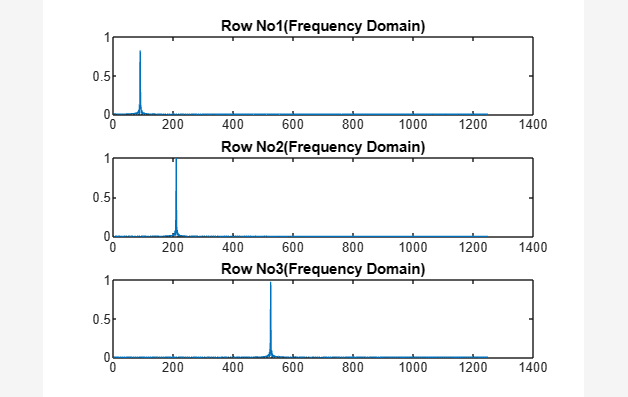
제목 ( [ '행 번호' , num2str ( 케이 ) , '(주파수 도메인)' ] )
끝
위의 코드에서는 시간 영역에서 출력 창에 r1, r2, r3의 세 가지 정현파가 표시됩니다. 주파수 도메인 신호 'PS1'은 각각의 개별 단면 진폭 스펙트럼을 계산하기 위해 파동에 FFT 기능을 사용하여 생성됩니다.
결론
그만큼 FFT 주파수 내용을 분석하여 신호를 다르게 이해하는 데 도움이 되는 유용한 도구입니다. MATLAB의 내장 함수인 fft를 사용하여 다음을 수행합니다. FFT 신호에 대한 계산이 편리해집니다. 이 기능을 사용하면 데이터를 시간 영역에서 주파수 영역으로 변환하여 서로 다른 주파수와 해당 주파수의 상대적 강도에 대한 중요한 세부 정보를 학습할 수 있습니다. 위의 가이드는 신호의 특성을 더 깊이 이해하고 다양한 애플리케이션에서 정보에 입각한 결정을 내리는 데 매우 중요합니다.